Jeremy Teitelbaum, dean of the College of Liberal Arts and Sciences, is a guest contributor to UConn Today. His posts appear on Mondays. For his previous posts, click here.
In his latest blog, “The Politics of Calculus,” my colleague Dean Jeremy Paul of UConn’s Law School laments our collective tendency to oversimplify our society’s problems and to view them as simple questions of, for example, “maximizing profit.” He calls for a public discourse that allows us to consider more than one variable at a time, and calls on all of us to pay more attention to “our friends in the math department” who know how to do this using Calculus.
It’s flattering to be called on to help heal society’s woes – mathematicians aren’t often put in that role – so I spent some time thinking about how a mathematical perspective might help improve our collective approach to societal problems. In response to Dean Paul’s shout-out, I offer three specific areas of mathematics that people don’t seem to properly appreciate, leading them to poor decision-making in many different areas of society. As it turns out, all three areas are even simpler than Calculus.
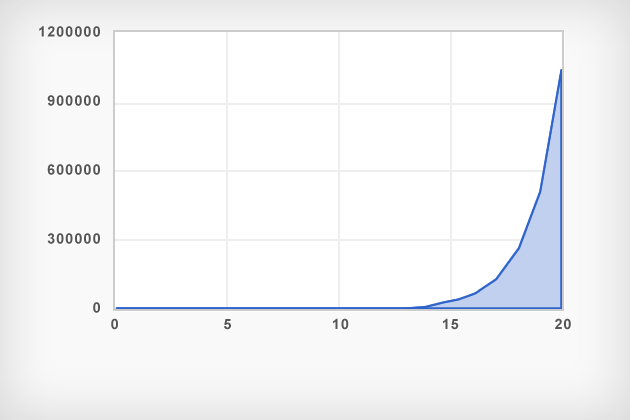
The first huge gap in our mathematical discourse concerns the process of exponential growth. Exponential growth is the process where a quantity increases by a fixed proportion every period, doubling, say, at a fixed interval. As the chart shows, exponential growth can seem very slow for a very long time before suddenly exploding.
The dramatic run-up in the price of Apple stock is a striking example of some people’s failure to grasp the explosive nature of exponential growth. As James Stewart explained in the New York Times, a continuing rate of 20 percent growth in Apple’s stock price over the next 10 years would lead to a market value in excess of the GDP of, say France. Beyond that, it wouldn’t take long for Apple to sell an iphone to every man, woman, child, and pet living on planet Earth. Such growth obviously will not continue – but many people are going to pay a high price for failing to appreciate that fact.
More broadly, we haven’t collectively appreciated that the same analysis applied to any fixed resource – like, say, fossil fuels – means that no amount of drilling will ever overcome an underlying exponential growth in demand. That growth in demand will eventually be impossible to satisfy.
The second area of mathematical knowledge that I’d like to see more widely appreciated is the notion of relative risk. We are very weird in our appreciation of risks. We turn our society upside down to minimize the risk of a terrorist attack, but we pick up our cell phones to send texts while driving down the highway. We buy guns to protect ourselves from intruders, vastly increasing the risk that one of our family members will use that gun to kill themself or accidentally kill or injure another family member. Some of us avoid vaccinating our children out of fear of side effects, putting them at much higher risk of dangerous diseases.
This inability to deal with relative risk has become a significant area of public debate recently, with the release of studies regarding the appropriate frequency of diagnostic tests such as mammograms and prostate cancer screenings. Many groups reacted with outrage and horror at suggestions that such tests be given less frequently or even not at all.
It seems obvious that more testing for dangerous diseases is better, and it’s difficult to suggest to someone that they wait longer before being tested. However, the tests themselves have risks, they are expensive, and they produce false positives leading to anxiety, even more testing, even more costs, and even more risks. In an ideal world, the public would have enough understanding of the science of relative risk to approach these problems deliberately, rather than jumping to the most simplistic conclusion that more testing, and earlier testing, is necessarily better.
The third type of mathematical knowledge that I wish was more widely understood isn’t really mathematics proper. Rather, it’s an appreciation for the fact that real world problems are amenable to analysis generally, and mathematical analysis in particular. Eugene Wigner, an important 20th-century physicist, wrote a famous essay called “The Unreasonable Effectiveness of Mathematics in the Natural Sciences,” in which he pointed out just how striking it is that mathematics – a product of abstract thought – should be so powerful as a tool for understanding the natural world. More recent developments in the social sciences, and even in areas like recommending music and movies, have shown that mathematics can be similarly powerful in other contexts as a tool for understanding the implications of different choices.
Dean Paul hopes that mathematical literacy will help us with the key questions that confront our democracy. Certainly mathematics provides tools – the methods of probability and statistics, the study of exponential growth, and many other concepts – that can help illuminate the world we live in. But to realize that potential, we need to be more than literate, we need to apply what we know. And that means we need to stop and think, hard, about what to do about our major problems before leaping to a plan of action. Unfortunately, that willingness to do some hard thinking seems even rarer than a knowledge of Calculus.