A snowflake is the nastiest well-behaved curve we can think of. And that’s a useful thing, argues UConn mathematician Vyron Vellis.
The snowy weather has snowflakes on our minds, though perhaps not the mathematical kind. Mathematical functions called Rohde snowflakes are different than your typical wintry precipitation. They’re made of triangles instead of ice, and they don’t melt in spring. But they can look very similar:
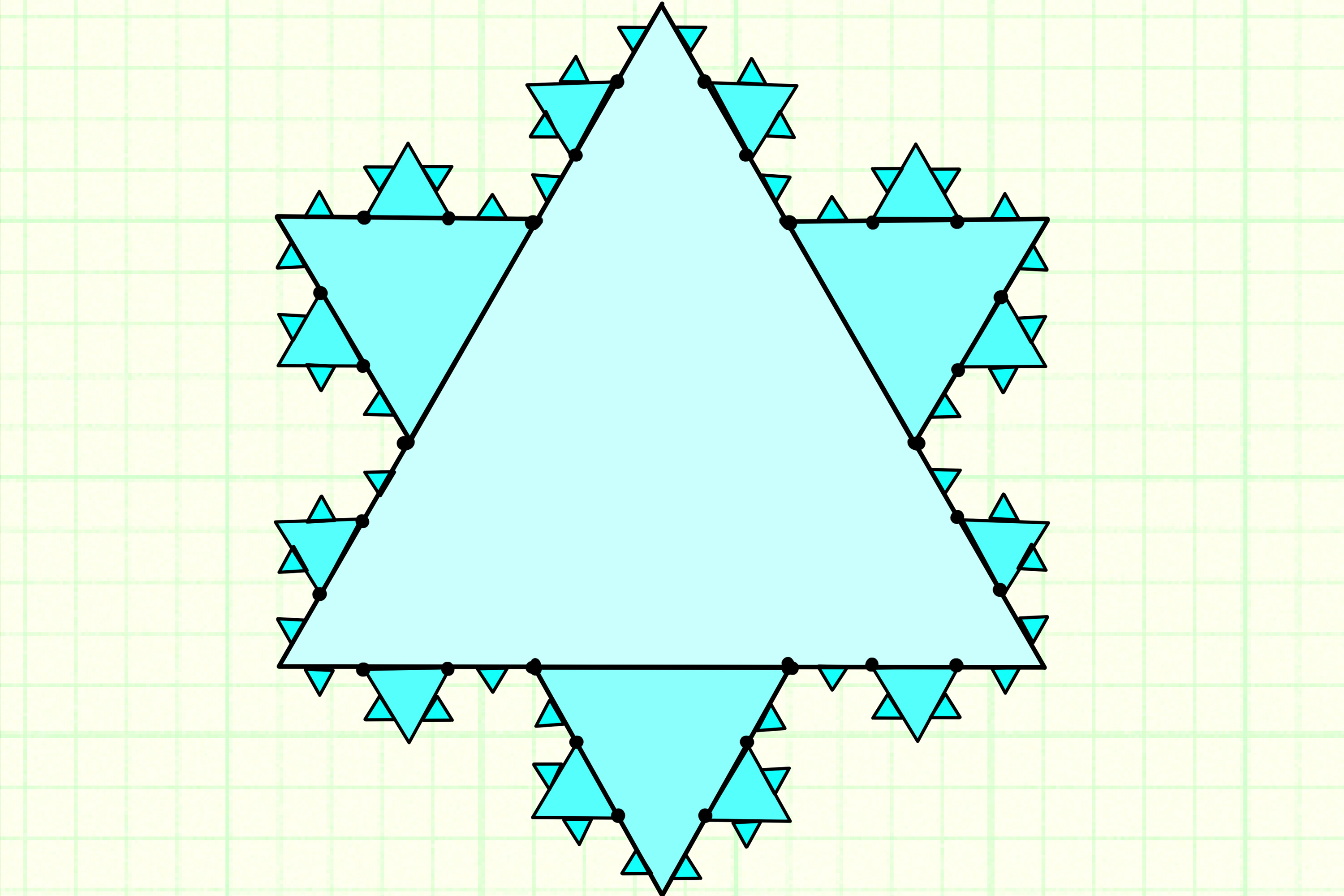
 The snowflake in the line drawing is one of the most famous in mathematics. It’s called a von Koch snowflake, and it’s a form of mathematical curve known as a fractal curve. To make it, you draw an equilateral triangle. Then you pop out smaller equilateral triangles on each of the original’s three sides. Then you pop out more triangles on those triangles’ side, and so on ad infinitum. This makes an infinitely long shape that looks the same at any scale, no matter how far you zoom in. It always looks like a Star of David, with an infinite array of smaller stars growing out of every side.
The snowflake in the line drawing is one of the most famous in mathematics. It’s called a von Koch snowflake, and it’s a form of mathematical curve known as a fractal curve. To make it, you draw an equilateral triangle. Then you pop out smaller equilateral triangles on each of the original’s three sides. Then you pop out more triangles on those triangles’ side, and so on ad infinitum. This makes an infinitely long shape that looks the same at any scale, no matter how far you zoom in. It always looks like a Star of David, with an infinite array of smaller stars growing out of every side.
Not all snowflakes are so symmetrical. Snowflakes can pop out different shaped triangles on different sides, or leave one side unmolested at every stage, but they are always formed by some combination of triangles spawning more triangles on their sides, infinitely. Their infinite length is what makes them nasty in Vellis’s opinion. However, they can be useful in math. Last year, Vellis, an assistant research professor, used snowflakes to prove some things about quasicircles. Quasicircles are much funkier mathematical objects, and not as well understood as snowflakes. But since he has proven that all snowflakes are quasicircles, mathematicians can now check theorems about quasicircles against snowflakes. Makes the math easier, and prettier.
Vellis was thinking about snowflakes and quasicircles because he does a lot of work with quasiconformal maps. Such maps can turn nice, simple objects like a circle or straight line into complicated objects like snowflakes. But they’re not just toys for mathematicians. Quasiconformal mapping is also used by materials scientists. They like it because it lets mathematical functions stretch a little, but not beyond recognition.

Quasiconformal mapping better reflects the real world, where molecules have certain shapes and can only stretch or bend so much. Quasiconformal analysis lets scientists figure out the limits of materials’ bending ability, to design things like better antennas or lenses. Or invisibility cloaks.
Coming back to snowflakes, Vellis admits they have other nice properties. For example, imagine a line with a dot bouncing around it.
“That dot goes everywhere, crazy. A random walk. Since our line is symmetrical, the point can hit the upper or lower edge with equal probability,” says Vellis. The same holds true for snowflakes. If you cut a snowflake somewhere along its length, that crazy bouncing point has a comparable probability of hitting the inside or the outside, despite the snowflake’s wildly crinkled shape and infinite length. Unintuitive, but true.
This property makes snowflakes useful for mathematicians as a test case for all curves, not just quasicircles. If you have a theorem in mind you believe holds true for all possible curves, you may want to test it against a snowflake, because they’re the worst possible good curves we can think of.