Whoever said rules were made to be broken wasn’t a physicist. When something doesn’t act the way you think it should, either the rules are wrong, or there’s new physics to be discovered. Which is exactly what UConn’s Connor Occhialini ’18 (CLAS), an honors student majoring in physics and math, found when he began researching scandium fluoride.

Scandium fluoride is a transparent crystal with a cubic shape, a byproduct of mining. It’s not used commercially and it wouldn’t be particularly interesting to anyone except for one odd thing: it shrinks as it warms.

Most materials swell as they heat up. Really simple materials like hydrogen gas swell because the heat makes their atoms zoom around faster, bumping into each other more, so the same number of hydrogen atoms need more space. More complicated materials also swell, which is why your wooden front door tends to stick in the summertime. But solids like wood can’t swell as much as a gas because their atoms are tightly linked together into long, interlocked molecules, so they just jiggle around, swelling the door a little bit.

Scandium fluoride must be doing something else, reasoned Occhialini. His advisor for his honors physics project, Jason Hancock, had been working with scandium fluoride, and asked Occhialini to study a model of the crystal’s dynamics. Scandium fluoride has a pretty simple structure: it’s a solid crystal, with each scandium atom surrounded by six fluorines to make stacks of octahedra (eight-sided diamonds). The researchers hoped the simple structure might be easy to understand. Understanding scandium fluoride’s strange ‘negative thermal expansion’, as physicists call the heat-related shrinkage, might yield more general insight into other, more complex materials that do the same thing.

Occhialini’s first step was to simplify the problem. So instead of a three-dimensional crystal, he decided to think about it as a two-dimensional sheet that looks like this:

Each black diamond represents a molecule of scandium fluoride. The scandium atoms (blue dots) are at the center of each diamond, and a fluorine atom is at each corner.

Most of the time, bonds between atoms are flexible. So in a normal crystalline solid – calcium fluoride, for example – the fluorines and calcium atoms would all be able to wiggle around independently when the material warmed up. As they wiggled, they’d take up a little more space, and the solid would swell. Normal solid behavior.

But Occhialini wondered if maybe that wasn’t what was happening in scandium fluoride. Maybe in this model, he should assume the bonds connecting each fluorine to its scandium were stiff? So stiff the fluorine-scandium bonds don’t move at all, so the diamonds are like solid blocks. The only places the structure would be able to flex when it warmed up would be at the fluorine atoms, which would act like tiny little joints. As the crystal heated up, the little scandium fluoride blocks would tilt around the fluorines at the corners. That’s what you see happening in the picture. You’ll notice that when the diamonds tilt, the whole structure gets smaller. It actually tightens up. The blue outline shows the structure at its coldest, perfectly ordered state, with no molecular motion. When the diamonds tilt, they take up a smaller total volume than the blue outline delineates. This is negative thermal expansion.

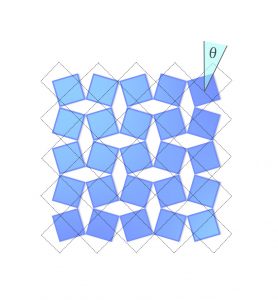
Occhialini figured out that you can describe this shrinkage mathematically, using just the angle of the molecules’ tilt. He called the angle Θ (theta). When the scandium fluoride blocks tilt by an angle Θ, the distance between the center of each block shortens by a factor of cosine Θ, and the crystal’s total volume shrinks.

To calculate that shrinkage (or, in a normal material, expansion) in detail, Occhialini added a third term to the classic equation that describes the energy of a vibrating crystal. The first two terms in the standard equation describe the potential energy a crystal has from the bending at each molecular junction, plus the kinetic energy of rotation of each molecule. Occhialini’s equation also describes the translational kinetic energy of the molecules–not just from rotating around, but also moving toward and away from their original positions as they rotate. The further they are from the center of mass of the crystal, the more they move. Look back at Figure 1 and notice the dot in the middle; that’s the center of mass. The diamonds in the middle barely move in relation to it, while the diamonds at the edges move a lot. Now imagine how much of a difference there would be if the crystal had millions of molecules instead of just 25. And now you understand how important that third term could be to the energy of the crystal.

Now, molecules being molecules, they don’t just shrink and stay there. They’re moving constantly, and the warmer they get, the more they move. Part of Occhialini’s insight is that, on average, the molecular structure gets bendier the warmer it gets. So the molecules tilt more and spend more time at bigger values of Θ, closer to 45 degrees. After Occhialini thought it over for a while together with Hancock and physics Ph.D. students Sahan Handunkanda and Erin Curry, they realized there was a geometric shape that had the same mathematical description. It’s Archimedes’ spiral pendulum, and it looks like this:

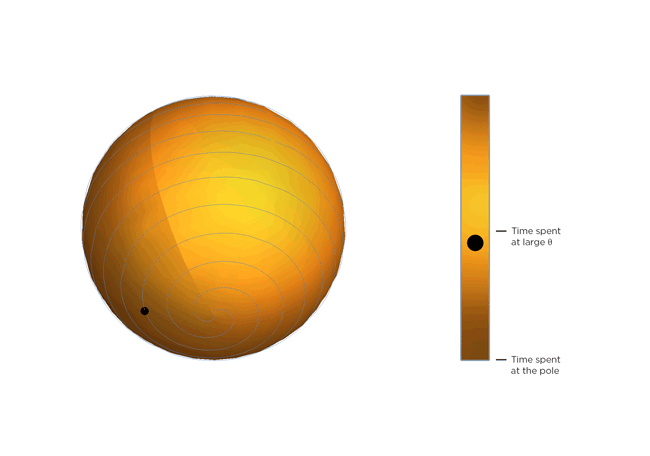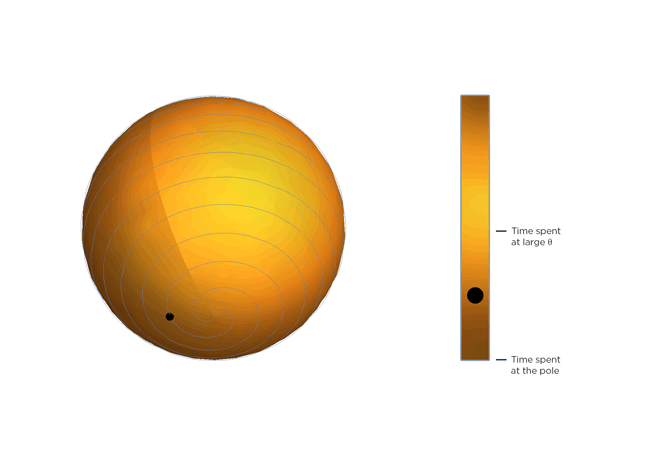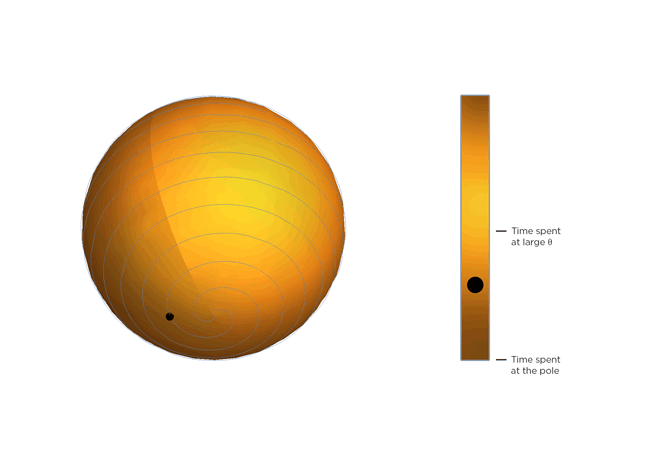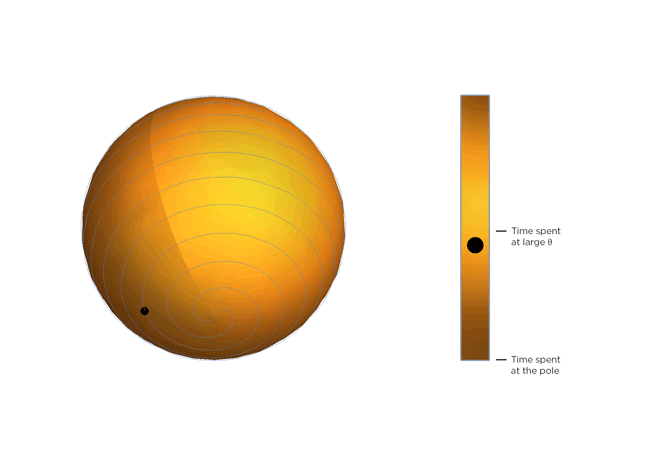
Each turning of the spiral is exactly the same distance from the last. That spacing – the distance between turns – is controlled by Θ. Imagine a line that stretches from the center of the sphere to a point on the spiral. The angle between that line and the pole of the sphere is Θ. You see the little ball traveling along the spiral? That’s the end of the imaginary line. As Θ gets bigger, the ball moves towards the equator. Imagine that the ball represents the instantaneous state of the scandium fluoride crystal – the physicists calculated the statistical average of what every molecule in the crystal is doing. You’ll notice the ball spends more time near the equator of the spiral sphere, that is, it tends to hang out where Θ is large. If the temperature of the crystal drops and the molecules wiggle less, Θ gets smaller, the more time the ball spends near the pole of the sphere and the less the crystal shrinks.

So not only can a really weird phenomenon of a crystal that shrinks as it warms be explained by just assuming the molecules are rigid, but it can be illustrated with a classical geometric shape!

Occhialini was just a freshman when Hancock introduced him to the scandium fluoride puzzle. He had to learn the math as he went, but after about two semesters of working on it he’d figured out the equation that described what was going on. Now in his senior year, he says his research experiences in Hancock’s lab have been integral to his experience as an undergraduate.

The equation works beautifully and explains certain aspects of Hancock’s experimental x-ray measurements as well.

“I learned a lot more doing research than any course could have given me,” Occhialini says.

And now you, dear reader, have learned a little bit, too.

Occhialini’s research has been funded through his advisor’s NSF grant no. DMR-1506825 and a SURF fellowship from the Office of Undergraduate Research. He was also named a Treibick Scholar.